TUTORIAL

VASP2KP

This package is used to automatically generate the k\cdot p Hamiltonians and the Zeeman's coupling and to calculate the values of all the parameters directly from the VASP calculations.

Tutorial video: https://www.bilibili.com/video/BV16fu6ePEuN/?vd_source=7ad173600937ab77607e3594ff291105

Directory:

1. Installation

The installation requires two steps. First, one needs to install the python package using pip. Second, download the patch and recompile VASP to generate vasp2mat.

1.1 Install VASP2KP

kdotp-generator is used in python package VASP2KP, which can be installed using pip:

pip install kdotp-generator

*If pip failed to install kdotp-generator in this way, you can download the source code of kdotp-generator from https://github.com/yjiang-iop/kdotp-generator then enter the file folder and excute

python setup.py install

Then VASP2KP is installed using pip:

pip install VASP2KP

* If pip failed to install VASP2KP, you can download the source code of VASP2KP then enter the file folder and excute

python setup.py install

Moreover, after installation, the post-processing python script mat2kp can be downloaded from https://github.com/zjwang11/VASP2KP.

1.2 Compile vasp2mat

vasp2mat are based on VASP of version 5.3 or 6.4.
If you want to generate the vasp2mat based on VASP of version 5.3, follow the steps below:

  1. Download the patch vasp2mat.5.3-patch-1.0.1.sh and put the file folders 'vasp.5.lib' and 'vasp.5.3' into the same file folder.
  2. Compile vasp.5.lib and vasp.5.3.
  3. run the patch vasp2mat.5.3-patch-1.0.1.sh:

    bash vasp2mat.5.3-patch-1.0.1.sh

The patch vasp2mat.5.3-patch-1.0.1.sh will generate a new file folder 'vasp2mat.5.3' which contains the necessary files to compile vasp2mat and then compile it. The target executable file vasp2mat is also contained in this file folder. After compiling, the directory structure is:

Directory Structure
vasp2mat_folder
│ vasp2mat.5.3-patch-1.0.1.sh
│
└─vasp.5.lib
│ │ Makefile
│ │ ...
│
└─vasp.5.3
│ │ Makefile
│ │ vasp
│ │ ...
│
└─vasp2mat.5.3
│ │ Makefile
│ │ vasp2mat
│ │ ...

If you want to generate the vasp2mat based on VASP of version 6.4, follow the steps below:

  1. Download the patch vasp2mat.6.4-patch-1.0.1.sh and put the file folder 'vasp.6.4' into the same file folder.
  2. Compile vasp.6.4.
  3. run the patch vasp2mat.6.4-patch-1.0.1.sh:

    bash vasp2mat.6.4-patch-1.0.1.sh

The patch vasp2mat.6.4-patch-1.0.1.sh will generate a new file folder 'vasp2mat.6.4' which contains the necessary files to compile vasp2mat in the file folder 'src' and then compile it. The target executable file vasp2mat is contained in the file folder 'bin' in this file folder. Moreover, if you use vasp-6.4, it is recommended to use Intel Fortran Compiler (mpiifort) 2022/2023 and makefile.include.intel for compilation. After compiling, the directory structure is:

Directory Structure
vasp2mat_folder
│ vasp2mat.6.4-patch-1.0.1.sh
│
└─vasp.6.4
│ │ makefile
│ │ makefile.include
│ │ bin
│ │ build
│ │ src
│ │ ...
│
└─vasp2mat.6.4
│ │ makefile
│ │ makefile.include
│ │
│ └─bin
│ │ │ vasp2mat
│ │ build
│ │ src
│ │ ...

2. Instruction with example for Bi2Se3

This part is the simple instruction of vasp2mat and mat2kp. Before using vasp2mat and mat2kp, we should first do self-consistence field calculation by VASP to get CHGCAR, and then do band calculation to obtain eigenenergies and wavefunctions of the specific wave vectors, i.e., EIGENVAL and WAVECAR. To prepare for the calculation of Löwdin partitioning, the parameter NBANDS in the band calculation input file INCAR should be set to a large number, and the input file KPOINTS should be set as

Bi2Se3
1
Reciprocal lattice
0 0 0 1.0

The former 3 numbers of the fourth line must be the specific wave vector to get k\cdot p Hamiltonian and Zeeman's coupling.

2.1 instruction of vasp2mat

2.1.1 Inputs of vasp2mat

To construct k\cdot p Hamiltonian and Zeeman's coupling, vasp2mat can be used to calculate the matrices of the generalized momentum, spin and the corepresentation of symmetry operators.

There are 6 input files of vasp2mat: POSCAR, POTCAR, KPOINTS, INCAR, WAVECAR, INCAR.mat. POSCAR and POTCAR are the same as VASP input files, and KPOINTS is the same as band calculation input file. WAVECAR was obtained by the band calculation with LWAVE=.TRUE. in INCAR. One has to change the set LWAVE=.FALSE. in INCAR to run vasp2mat, in case the WAVECAR is not erased.

2.1.1.1 INCAR.mat

The input file of vasp2mat which contains the matrix information is INCAR.mat.
In INCAR.mat, there are many parameters we should set:

  • vmat: Calculation selection. The main choises are:
    • 10: Calculate the matrices of the spin operator.
    • 11: Calculate the matrices of the generalized momentum operator.
    • 12: Calculate the corepresentation matrices of time reversal or crystalline symmetry operators.
  • vmat_name: The name of the crystalline symmetry operator, or 'Pi' for generalized momentum matrices calculation, or 'sig' for spin matrices.
  • bstart: The start id of the bands to calculation matrices.
  • bend: The end id of the bands to calculation matrices.

If vmat is set to 12, there are more parameters we should set:

  • rot_n: The vector of the rotational axis of the symmetry operator.
  • rot_alpha: The rotation angle in degrees.
  • rot_det: The determinant of the O(3) matrix of the symmetry operator (if a spatial inversion exists or not).
  • rot_tau: The space translation part of the symmetry operator.
  • time_rev: If there is a time reversal in the symmetry operator.

These parameters are related to the space group operators in OUTCAR of the band calculation, which is shown below for Bi2Se3:

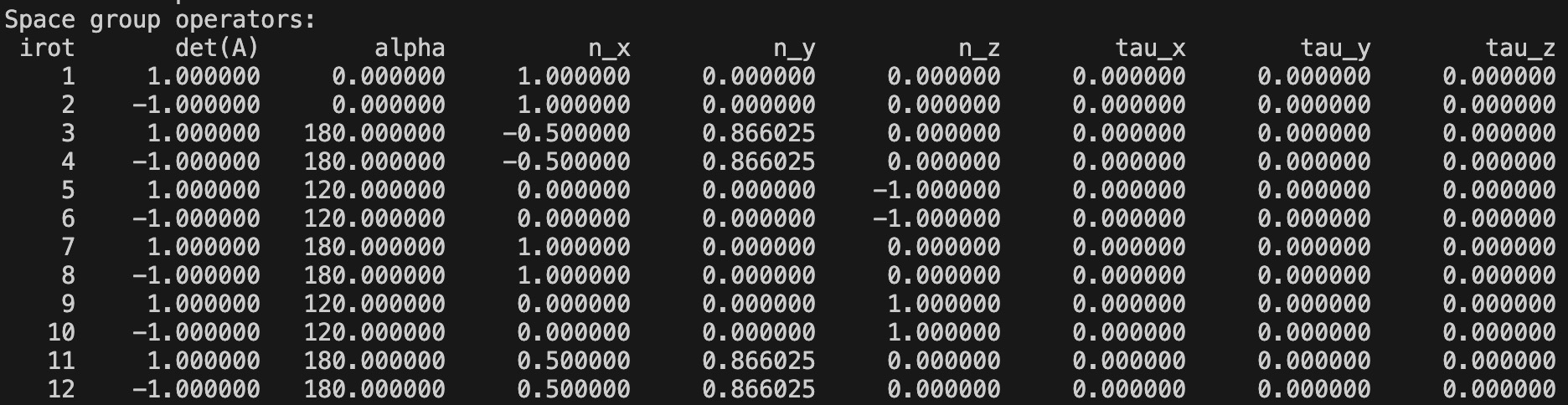
Other parameters are no need to be changed as the INCAR.mat below. For the construction of k\cdot p Hamiltonian and Zeeman's coupling for Bi2Se3, the matrices of generalized momentum \hat{\pi} and spin \hat{s}, as well as the matrices of generators of the little group, i.e., C_{3z}, C_{2x}, P and T, should be calculated.
INCAR.mat for calculation of generalized momentum matrices is

&vmat_para
! soc------------------------------------------
cfactor=1.0
socfactor=1.0
nosoc_inH = .false.
! operator-------------------------------------
vmat = 11
vmat_name = 'Pi'
vmat_k = 1
bstart=1, bend=400
print_only_diagnal = .false.
/

The output file MAT_Pi.m contains the matrices of \pi_x, \pi_y and \pi_z, in the unit of \hbar/a, where \hbar is the reduced Planck constant and a is the Bohr radius.

INCAR.mat for calculation of spin matrices is

&vmat_para
! soc------------------------------------------
cfactor=1.0
socfactor=1.0
nosoc_inH = .false.
! operator-------------------------------------
vmat = 10
vmat_name = 'sig'
vmat_k = 1
bstart=47, bend=50
print_only_diagnal = .false.
/

The output file MAT_sig.m contains the matrices of s_x, s_y and s_z, in the unit of \hbar/2, where \hbar is the reduced Planck constant. In other words, there are the matrices of Pauli operator \hat{\sigma}.

To calculate the corepresentation matrix of the crystalline symmetry operator C_{3z}/C_{2x}/P/T, the input files INCAR.mat are

&vmat_para
! soc------------------------------------------
cfactor=1.0
socfactor=1.0
nosoc_inH = .false.
! operator-------------------------------------
vmat = 12
vmat_name = 'C3z'                     !/   'C2x'   /   'P'   /   'T'  
vmat_k = 1
bstart=47, bend=50
print_only_diagnal = .false.
! rotation-------------------------------------
rot_n(:) = 0 0 1                     !/   1 0 0   /   0 0 1   /   0 0 1  
rot_alpha = 120                     !/   180   /   0   /   0  
rot_det = 1                           !/   1   /   -1   /   1  
rot_tau(:) = 0 0 0
rot_spin2pi = .false.
time_rev = .false.                     !/   .false.   /   .false.   /   .true.  
/

Notice: Running vasp2mat once can only compute the representation matrix of one operator, so you should run vasp2mat many times to obtain all representation matrices of the generators.

2.1.2 Run vasp2mat

Put 6 input files of vasp2mat into the same file folder, and run vasp2mat:

vasp2mat

After waiting a few minutes, vasp2mat will finish calculating. Notice: It does not take much time to compute matrices using vasp2mat, so vasp2mat does not support parallel computing now. Therefore, you should not use mpi liken 'mpirun -np 2 vasp2mat'.

2.1.3 Outputs of vasp2mat

The main input file of vasp2mat is 'MAT_XXX.m', which contains the matrices of the specific quantity. XXX is the same as vmat_name in INCAR.mat. 'MAT_XXX.m' is the source file of matlab, thus can be directly run by it.

2.2 Instruction of mat2kp

2.2.1 Inputs of mat2kp

2.2.1.1 Input data files

As the input files of the main function get_std_kp_Zeeman, the eigenenergies EIGENVAL and the matrices files XXX.m obtained by VASP and vasp2mat should be put into a file folder. For instance, for Bi2Se3, the directory structure can be set as

Directory Structure
Bi2Se3
│ mat2kp.in
│
└─GMmat
│ │ EIGENVAL
│ │ MAT_Pi.m
│ │ MAT_sig.m
│ │ MAT_C3z.m
│ │ MAT_C2x.m
│ │ MAT_P.m
│ │ MAT_T.m

2.2.1.2 mat2kp.in

Necessary parameter

There is a necessary parameter of mat2kp.in, Symmetry, which has the same structure of a python dictionary, whose keys must be the same names of the symmetry operators of the inputs of mat2kp, and its values are also python dictionaries. The keys of the values of Symmetry are:

  • rotation_matrix: the O(3) (real-space) rotation matrix of the operation.
  • repr_matrix: the standard corepresentation matrix of the operation, either reducible or irreducible.
  • repr_has_cc: a boolean flag to determine whether the operation is unitary or anti-unitary. If repr_has_cc=True, the operation becomes g*T, with g being unitary and specified in rotation_matrix, and repr_matrix contains a complex conjugation.

Both rotation_matrix and repr_matrix should use Matrix(). The non-integer numbers a/b should be typed by Rational(a/b). \sqrt{a} should be typed by sqrt(a). The constant \pi should be typed as pi and imaginary unit i should be typed as I. If there are exponential numbers, converting them to square numbers is more efficient to compute, e.g., e^{i\pi/4}=(\sqrt{2}+\sqrt{2}i)/2.

Optional parameters

There are 6 optional parameters in mat2kp.in:

  • vaspMAT: the path of the file folder which contains the input data files. The default value is 'mat'.
  • order: the order of k\cdot p Hamiltonian to be constructed, 2 (default) or 3.
  • print_flag: where to output the results: 1 (screen) or 2 (files, default).
  • kpmodel: whether to compute kp Hamiltonian: 0 (no) or 1 (yes, default).
  • gfactor: whether to compute Zeeman's coupling: 0 (no) or 1 (yes, default).
  • log: whether to output the log files: 0 (no) or 1 (yes, default).

mat2kp.in for Bi2Se3
Symmetry = {
'C3z' : {
'rotation_matrix':
Matrix([[-Rational(1,2), -sqrt(3)/2,0],[sqrt(3)/2, -Rational(1,2), 0],[0, 0, 1]]),
'repr_matrix':
Matrix([[Rational(1,2)-I*sqrt(3)/2,0,0,0],[0,Rational(1,2)+I*sqrt(3)/2,0,0],
[0,0,Rational(1,2)-I*sqrt(3)/2,0],[0,0,0,Rational(1,2)+I*sqrt(3)/2]]),
'repr_has_cc': False},
'C2x' : {
'rotation_matrix': Matrix([[1, 0, 0],[0, -1, 0],[0, 0, -1]]),
'repr_matrix':
Matrix([[0,-Rational(1,2)-I*sqrt(3)/2,0,0],[Rational(1,2)-I*sqrt(3)/2,0,0,0],
[0,0,0,-Rational(1,2)-I*sqrt(3)/2],[0,0,Rational(1,2)-I*sqrt(3)/2,0]]),
'repr_has_cc': False},
'P' : {
'rotation_matrix': Matrix([[-1,0,0],[0, -1, 0],[0, 0, -1]]),
'repr_matrix':
Matrix([[1,0,0,0],[0,1,0,0],[0,0,-1,0],[0,0,0,-1]]),
'repr_has_cc': False},
'T' : {
'rotation_matrix': eye(3),# Identity Matrix
'repr_matrix': Matrix([[0,1,0,0],[-1,0,0,0],[0,0,0,-1],[0,0,1,0]]),
'repr_has_cc': True}
}
# optional parameters
vaspMAT = '../Bi2Se3/GMmat' # the path: to read eigenvalues, Pi, s, and R matrices in this folder.
order = 2 # Order of the kp model : 2 (default) or 3.
print_flag = 2 # Where to output results: 1 (screen) or 2 (files, default).
kpmodel = 1 # Whether to compute Hkp: 0 or 1 (default).
gfactor = 1 # Whether to compute HZ: 0 or 1 (default).
log = 1 # Whether to output log files: 0 or 1 (default).

2.2.2 Run mat2kp

After preparing all the inputs of mat2kp, run mat2kp at the same folder as mat2kp.in:

mat2kp

If order is set to be 2, then it will take about 1 minute for mat2kp to finish calculating.
If order is set to be 3, then it may takes a few hours for mat2kp to finish calculating.

2.2.3 Outputs of mat2kp

There are 3 output files of mat2kp, 'kp-parameters.out', 'g-factors.out' and 'kp_Hamiltonian-Zeeman's_coupling.tex'.

2.2.3.1 kp-parameters.out

This file contains the k\cdot p Hamiltonian of each order as well as the calculation error.
'kp-parameters.out' for Bi2Se3:

kp Hamiltonian
========== Result of kp Hamiltonian ==========
Matrix([[a1 + a2 + c1*(kx**2 + ky**2) + c2*(kx**2 + ky**2) + c3*kz**2 + c4*kz**2, 0, -I*b2*kz, -b1*(kx*(sqrt(3) + 3*I) + ky*(3 - sqrt(3)*I))/3], [0, a1 + a2 + c1*(kx**2 + ky**2) + c2*(kx**2 + ky**2) + c3*kz**2 + c4*kz**2, b1*(kx*(sqrt(3) - 3*I) + ky*(3 + sqrt(3)*I))/3, I*b2*kz], [I*b2*kz, b1*(kx*(sqrt(3) + 3*I) + ky*(3 - sqrt(3)*I))/3, a1 - a2 + c1*(kx**2 + ky**2) - c2*(kx**2 + ky**2) + c3*kz**2 - c4*kz**2, 0], [-b1*(kx*(sqrt(3) - 3*I) + ky*(3 + sqrt(3)*I))/3, -I*b2*kz, 0, a1 - a2 + c1*(kx**2 + ky**2) - c2*(kx**2 + ky**2) + c3*kz**2 - c4*kz**2]])
Parameters:
a1 = 4.8898 ;
a2 = -0.2244 ;
b1 = -3.238 ;
b2 = 2.5562 ;
c1 = 19.5842 ;
c2 = 44.4746 ;
c3 = 1.8117 ;
c4 = 9.5034 ;
Error of the linear least square method: 3.93e-06
Sum of absolute values of numerical zero elements: 6.47e-02

2.2.3.2 g-factors.out

This file contains the Hamiltonian matrix of Zeeman's coupling as well as the values of all parameters.
'g-factors.out' for Bi2Se3:

Zeeman's coupling
========== Result of Zeeman's coupling ==========
mu_B/2*Matrix([[Bz*g3 + Bz*g4, g1*(Bx*(1 - sqrt(3)*I/3) + By*(-sqrt(3)/3 - I)) + g2*(Bx*(1 - sqrt(3)*I/3) + By*(-sqrt(3)/3 - I)), 0, 0], [g1*(Bx*(1 + sqrt(3)*I/3) + By*(-sqrt(3)/3 + I)) + g2*(Bx*(1 + sqrt(3)*I/3) + By*(-sqrt(3)/3 + I)), -Bz*g3 - Bz*g4, 0, 0], [0, 0, Bz*g3 - Bz*g4, g1*(Bx*(1 - sqrt(3)*I/3) + By*(-sqrt(3)/3 - I)) + g2*(Bx*(-1 + sqrt(3)*I/3) + By*(sqrt(3)/3 + I))], [0, 0, g1*(Bx*(1 + sqrt(3)*I/3) + By*(-sqrt(3)/3 + I)) + g2*(Bx*(-1 - sqrt(3)*I/3) + By*(sqrt(3)/3 - I)), -Bz*g3 + Bz*g4]])
Parameters:
g1 = -0.3244 ;
g2 = 5.7610 ;
g3 = -7.8904 ;
g4 = -13.0138 ;
Error of the linear least square method: 6.11e-08
Sum of absolute values of numerical zero elements: 4.12e-03

2.2.3.3 kp_Hamiltonian-Zeeman's_coupling.tex

This file is the latex source file, which contains all the matrix elements and the values of all parameters of k\cdot p Hamiltonian and Zeeman's coupling. If the system has already installed the latex compiler, mat2kp will automatically compile this source file to generate 'kp_Hamiltonian-Zeeman's_coupling.pdf'. This file is quite long, therefore we do not show it here.

2.2.4 Log files

If log is set to be 1, mat2kp will generate 3 log files: 'find_similarity_transformation_matrix.log', 'independent_kp_models(without numerical parameters).log' and 'independent_Zeeman's_coupling(without numerical parameters).log'.

2.2.4.1 find_similarity_transformation_matrix.log

The log file 'find_similarity_transformation_matrix.log' records errors of each step of the optimization process of unitaryizing, where the error is defined as \varepsilon = \sum_{ij}\left|(U^{\dagger}U-I)_{ij}\right|, U is the similarity transformation matrix while I is the identity matrix of the same size of U. At the end of this file, the result of the similarity transformation matrix and errors of each generator's matrix are presented. The error of generator R's matrix is given by \varepsilon(R)=\sum_{ij}\left|(U^{\dagger}D^{\text{num}}(R)U-D^{\text{std}}(R))_{ij}\right|.

2.2.4.2 independent_kp_models(without numerical parameters).log

The log file 'independent_kp_models(without numerical parameters).log' records the output and warning while using the function kdotp_generator.symmetric_hamiltonian of python package kdotp-generator in the process of generating the analytical k\cdot p Hamiltonian. In this log file, we can find the independent k\cdot p models with their matrix basis and polynomial basis of k of each order. The detailed description of the output of kdotp_generator.symmetric_hamiltonian can be viewed in the introduction of python package kdotp-generator.

2.2.4.3 independent_Zeeman's_coupling(without numerical parameters).log

The log file 'independent_Zeeman's_coupling(without numerical parameters).log' records the output and warning while using the function kdotp_generator.symmetric_hamiltonian of python package kdotp-generator in the process of generating the analytical Zeeman's coupling.
If the optional parameter gfactor is set to be 0, this log file will no longer be generated.